пробный выпуск, январь 1998

АСПЕКТЫ ВЫБОРА

Данный методический подход к решению задач заимствован из замечательных работ Л.В.Тарасова и А.Н.Тарасовой "Вопросы и задачи по физике" и Г.Остера "Физика". В отличие от изложения Л.В.Тарасова и А.Н.Тарасовой в задачах не приводится окончательного мнения преподавателя, а к некоторым задачам Г.Остера добавлено физическое содержание, при максимальном сохранении авторской интонации текста.

Предлагаемый метод решения задач основан на реальной человеческой ситуации выбора. Только выбирать нужно не между "да" или "нет", угадывая ответ, а выбирать подход или путь к ответу.

Каждый человек достаточно многогранен в своей умственной и психической деятельности, и какая грань проявляется при решении той или иной задачи, зависит от многих, как внешних, так и внутренних условий. Надеемся, что после изучения предлагаемого курса уменьшится количество равнозначных вариантов решений, которые возникают перед учеником, читающим условие задачи.

Предполагается, что задачи будут решаться малыми группами или подобными методами. Часть решений заведомо неправильна, но могут для одной задачи встречаться и несколько правильных решений, точно также, как и есть задачи, для которых не приведено ни одного правильного решения. В предлагаемой работе собраны наиболее достоверные способы решения задач, которые предлагали ученики и учителя.

Более отдаленные последствия, очевидно, заключаются в формировании навыков анализа решения, и критериев их отбора. Преподаватель ставит себе цель добиться от учеников даже не правильного выбора решения задачи, а правильной формулировки проблемы, решаемой сетью противоречивых и разветвленных вопросов — ответов. Для достижения цели были опробованы следующие методы:

1. вместо контроля знаний и умений по пройденной теме составляется из предложенных задач задание для самостоятельной или домашней работы;

2. на уроке группе ребят предлагается составить решение задачи из предложенных решений или предложить собственное решение с обязательным его анализом.

Что можно сказать о реакции школьников на эти методологические подходы? Во-первых, всем ученикам нравятся веселые, ироничные условия задач и картинки к ним. Во-вторых, дифференциация выбора решения в зависимости от подготовленности и способностей конкретного учащегося: ученикам со слабыми знаниями больше нравится вместо решения каламбур Фразера, средние ученики предпочитают выбрать одно из предложенных решений, на их взгляд правильное, способные ученики, с приличным знанием темы, пытаются составить решение из нескольких предложенных да еще прибавить что-то свое. Окончательное мнение по приведенной методике еще не сформировалось, но увеличение навыков рассуждать и к месту и без него обнаруживалось достаточно надежно.

Для примера приведем несколько задач подобного типа.

.

Задача 2

Старый и молодой охотники вышли из дома на лыжах искать медведя. Сначала прошли 10 км в южном направлении, где и встретили небольшого медведя. "Убьем?"- спросил молодой охотник. "Нет, мы ищем большого медведя", — ответил старый охотник. Они прошли еще 10 км на юг и встретили другого медведя, которого тоже сочли худосочным. Охотники повернули на восток и, пройдя 5 км, обнаружили большущего медведя. Старый охотник выстрелил в лапу медведя, и, повернув на север, охотники, преследуемые медведем, быстро побежали. Через 15 км медведь стал их настигать, и молодой охотник, вспомнив о своем заряженном ружье, убил медведя. "Что ты наделал! — сказал старый охотник. — Нам его еще 5 километров на себе тащить придется до дому".

Определить:

а) среднюю скорость передвижения охотников;
б) цвет медведя;
в) какое положение ТРИЗа не успел втолковать старый охотник молодому?

Охотники искали медведя со скоростью V₁ = 5 км/ч; убегали от медведя со скоростью V₂ =10 км/ч; тащили медведя со скоростью V₃ = 1 км/ч.

Эвристик: Из теории размерности можно составить однозначную комбинацию для нахождения средней скорости, в которой время для каждого участка пути находится по известной формуле для равномерного движения:

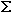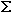V_ср = S_i / t_i 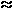2,6 км/ч (1)

Теория размерности ничего не может сказать о цвете медведя, но, по теории вероятности, медведь, скорее всего, был бурый. Отвечая на последний вопрос задачи, замечу, что с точки зрения ТРИЗа любая техническая система стремится к идеальности. Для достижения идеального результата охотникам не хватило 5 км.

Саша: Эвристик всегда решал так просто, а сейчас что-то все усложнил. Моя формула гораздо короче. Найдем среднюю скорость, как среднюю арифметическую известных скоростей:

V_ср = (V₁ + V₂ + V₃) / 3 = 5,3 км / час.

Цвет медведя из формулы не следует, а ТРИЗ для охоты вообще бесполезная штука.

Тимофей: Эвристик, следуя теории размерности, написал в данном случае верное решение, потому что и мое такое же. Меня совсем не устраивает короткое решение Саши. Но почему медведь бурый? Я бы выбрал для медведя черный цвет. Охота могла происходить и на гималайского медведя. А что касается ТРИЗа, в любом виде деятельности, в том числе и охоте, нужно наиболее полно использовать ресурсы.

Фразер: Средняя скорость убегания охотников, охотившихся на охоте на медведя, должна быть не менее 50 км / час. Иначе медведь их скушает. А с точки зрения ТРИЗа, по закону согласования, цвет медведя должен быть близким к цвету окружающего его снега. В противном случае ему будет трудно на охоте охотиться на охотников.

.

Задача 9

Однажды в понедельник идеальный газ, привычно расширяясь, затосковал от монотонной работы и решил пойти другим путем: вместо прямой в координатах PV, он описал квадрат, в котором прежняя прямая занимала место диагонали. Когда идеальному газу пришлось больше поработать, если экстремальные значения температур и объемов отличаются, соответственно, в 4 и в 2 раза?

Эвристик: Из чертежа (на рис. 1) видно, что отношение работ равно отношению площадей трапеции и квадрата. Очевидно, что площадь трапеции больше площади квадрата не более чем в 10 раз, так как объемы и температуры не слишком отличаются.

Рис. 1

Саша: После того, как Эвристик нарисовал график, совсем нетрудно подсчитать и точное отношение работ. Запишем формулу для площади трапеции:

А₁ = 1/2 (Р₁ + Р₂) (V₁ - V₂) (1)

После элементарных преобразований для одного моля газа получим:

А₁ = 1/2 R (T₂/2 + T₁) (2)

где Т₁ и Т₂ — температуры соответствующих состояний газа 1 и 2. Аналогичны рассуждения для квадрата:

А₂ = (Р₂ - Р₁) (V₂ - V₁) (3)

После преобразований получим:

А₂ = R (T₂/2 - T₁) (4)

Из сравнения соотношений (4) и (2) видно, что А₁/А₂ = 3/2.

Тимофей: Предлагаю более простое решение. Теплоемкость газа в процессе, когда давление растет пропорционально объему, неизвестно. Поэтому для вычисления работы я воспользуюсь средним значением теплоемкостей при постоянном давлении с_p и объеме с_v:

А₁ = 1/2 (c_p + c_v) (T₂ - T₁). (5)

Подставив известные значения молярных теплоемкостей одноатомного идеального газа и соотношение температур, получим:

А₁ = 6 R T₁ (6)

Используя значение работы А₂, найденное Сашей, получим, что соотношение работ А₁/А₂ = 6, что существенно отличается от ответа Саши.

Света: Мне кажется, что в решении Тимофея допущена непростительная ошибка. Выражение (5), которое он считает работой, принято называть теплотой, так как оно содержит в себе внутреннюю энергию.

В соответствии с этим, скорректируем формулы Тимофея, отняв от его "работы" внутреннюю энергию:

U = 3/2 R (T₂ - T₁) (8)

Используя выражение (8), найдем окончательное выражение для работы А₁:

А₁ = 3/2 R T₁ (9)

что совпадает с решением Саши. Полученный результат говорит о том, что и упрощенные рассмотрения процессов могут давать ответы, совпадающие с точными решениями, если не забывать о такой мелочи, как первый закон термодинамики.

Эвристик: Да, здесь совершенно очевидно, что при постоянном давлении увеличивается внутренняя энергия и совершается работа, а при постоянном объеме работа не совершается. Поэтому и теплоты расходуется меньше, а количество теплоты пропорционально теплоемкости.

Фразер: Как говорится, "котлеты отдельно, гайки отдельно", газ идеальный или тоскующий? В общих чертах сформулируйте мне сначала определение идеального — тоскующего газа, а там уже можно и подумать.