
| | |
2.2.3.3 Моделирование задач-ловушек и управление психологической инерцией
Неумение выделять существенные признаки и работать с ними создает в сознании ученика постоянный "информационный шум". Существенные признаки "забываются", несущественные, наоборот, начинают определять ход решения. Анализ фонда задач на психологическую инерцию (ПИ), проведенный нашей ученицей [11], показывает, что большинство так называемых задач-ловушек связаны с мнимыми противоречиями, возникающими из-за неграмотной работы с признаками.
Готовый ресурс для анализа и решения задачи есть и известен решателю, но он может нечаянно:
- забыть существенный признак (например, ученик в процессе решения задачи получает стороны треугольника: 50 см, 10 см и 35 см - и не замечает ошибки);
- добавить новый признак, который на самом деле не является существенным (так, утверждая, что построить 3 точки, через которые нельзя провести окружность, невозможно, ученик неосознанно добавляет требование, чтобы 3 точки не лежали на одной прямой);
- ограничить спектр значений признака (иллюстрация - известная задача Капицы: "с какой скоростью должна бежать собака, чтобы не слышать звука сковородки, привязанной к ее хвосту?", решая которую, легко забыть, что скорость может равняться нулю);
- перепутать признаки разных элементов (например, в ошибочном рассуждении типа: "70:14=70:(7+7)=70:7+70:7=20" ученик неверно применяет распределительное свойство) и т.д.
Опираясь на определение объектов и на модель ЭПЗ можно учить детей решать ловушки и, что важнее, самостоятельно строить их, заранее отстраиваясь от ПИ [4,5,11].
Модель ЭПЗ обеспечивает основу для обучения исследовательской деятельности: сбору информации, ведению картотек, обучению наблюдениям, построению простых гипотез [13]. Использование 3 групп признаков (п. 2.2.2.) позволило разработать алгоритм построения модели объекта, который также планируется применять при обучении исследовательской деятельности [22]. Некоторые примеры простых моделей приведены ниже.
2.2.3.4 Обучение ведению картотек
Cбор и первичная обработка информации - особый этап исследовательской деятельности, требующий специального обучения. Ученики начальной и средней школы обычно плохо справляются с задачей конспектирования и реферирования источников информации, не могут сориентироваться в объемном тексте, выделить главное, существенное.
Опыт организации исследовательской деятельности школьников показывает, что сбор картотеки, состоящей из множества хорошо структурированных и небольших по объему порций информации позволяет сделать начальный процесс исследования мотивированным и доступным даже для учеников начальных классов.
На первых порах форма карточки (фактически это перечень признаков, существенных с точки зрения решения конкретной проблемы) задается учителем. Дети собирают и фиксируют информацию (пример - на рис.4). В дальнейшем форма карточки определяется совместно с детьми - во фронтальной работе, затем - в группах, и далее индивидуально.
|
Имя сказочного героя |
Чиполлино |
|
Где живет? |
В Италии |
|
Волшебные свойства |
Может заставить людей плакать |
|
Что умеет делать? |
Решать проблемы. |
|
На кого похож? |
На луковицу |
|
С кем дружит? |
С Вишенкой, Тыквой,… |
Рис. 4. Карточка из картотеки волшебных существ
2.2.3.5 Морфологический анализ объекта исследования, построение морфологических таблиц
Решая задачу синтеза новых объектов, можно эффективно использовать метод морфологического анализа. Пример коллективной поисковой работы по анализу и синтезу сказочных сюжетов в 6-м классе - в работе [21].
|
Герои |
Люди |
Животные |
Явления природы |
Черты характера |
… |
|
Цели |
Найти кого-то |
Добраться куда-то |
Жениться |
Раскрыть тайну… |
… |
|
Препятствия |
Непроходимый лес |
Высокие горы |
Запрет на какие-то действия |
… |
|
|
… |
|
|
|
|
|
Рис. 5. Морфологический ящик сказочных сюжетов (фрагмент)
Построение такого морфологического ящика позволило детям сочинять собственные сюжеты сказок.
* * *
Все модели, которые будут представлены ниже, могут быть описаны через модель Элемент - Признак - Значение, но обеспечивают существенно новые, по сравнению с нею, возможности, в частности - управление воображением и ценностный подход к проблеме.
2.3 Модель "точка зрения"
2.3.1 ОПИСАНИЕ МОДЕЛИ
"Люди воспринимают мир по-разному". Переведя эту фразу на "язык" признаков, можно утверждать, что в одних и тех же "элементах мира" мы видим различные существенные и характерные признаки в зависимости от проблем, через призму которых смотрим вокруг. Модель "точка зрения" позволяет, не нарушая целостности восприятия объекта, описывать его в разных моделях, с позиции разных участников и наблюдателей проблемной ситуации.
Чтоб построить модель "точка зрения", нужно определить особенности участника или наблюдателя конфликта и оценить задействованные в конфликте системы и их взаимодействия с этой позиции. При этом обязательно определится ценностное восприятие: конкретные значения признаков будут восприняты как положительные (+), отрицательные (-) или нейтральные (0).
Таким образом, модель "точка зрения", как своеобразный "прожектор" высвечивает и окрашивает отношением определенные признаки объекта, не требуя детального анализа и точного описания.
2.3.2 ПРОИЗВОДНЫЕ МОДЕЛИ И КОНТЕКСТЫ ПРИМЕНЕНИЯ
2.3.2.1 Модели "Реального мира" и "Зазеркалья" (построение и "естественнонаучной" и "образной" картин мира)
В начальной школе мы вводим представление о двух взглядах на объект: взгляд из "Реального мира" и из "Зазеркалья" (мира Образов) (рис.6).
В реальном мире объект предстает таким, каким мы получаем его в опыте, с реальными значениями признаков.
В Зазеркалье мы воспринимаем объект таким, каким он нам кажется. Исходя из своих ценностей, мотивов, настроения, мы отвечаем на вопрос "на что похож объект?" - и получаем метафорические, "зазеркальные" значения признаков. Так, если в "Реальном мире" ручка скользкая, выскакивает из рук, в "Зазеркалье" - у нее капризный нрав, если первый снег - рассыпчатый, тает в руках, в Зазеркалье он пугливый, легко ранимый…
|
Реальный мир: ЧТО ВИЖУ? ОСТРОВ |
Зазеркалье: НА ЧТО (НА КОГО) ПОХОЖ? НА ЧЕРЕПАХУ |
Рис.6. Пример рассмотрения объекта в Реальном мире и в Зазеркалье.
Позднее мы добавляли еще один взгляд - фантастический, допуская в реальной картине мира замену некоторых значений на нереальные (умение строить такого рода модели тоже с необходимостью следует из анализа проблемы) [25].
2.3.2.2 "Точка зрения" - основа для обучения построению модели анализа проблемы
С точки зрения ОТСМ-ТРИЗ для решения проблемы очень полезно осознавать ее как противоречие субъективных желаний человека объективным законам, управляющим поведением объекта, на которое эти желания направлены [25], поэтому обучение оценке ситуации с различных позиций необходимо для формулировки проблемы в виде противоречия.
2.3.2.3 "Ролевые модели"
"Ролевые модели" позволяют рассмотреть объект с точки зрения лица определенной профессии. Они обеспечивают полимодельное восприятие объекта исследования (текста на уроках литературы, художественного произведения на уроках МХК, информационной среды на уроках информатики). Примеры - на рис. 7 и 8.
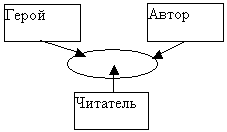
Рис.7. Ролевой подход к изучению литературных произведений
|
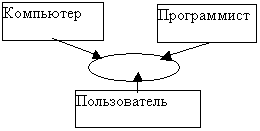
Рис.8. Ролевой подход к изучению информационной среды |
2.3.2.4 Шкала ценностей
|
Обучение построению шкал - отдельная проблема, которую можно, на наш взгляд, эффективно решать, базируясь на модели "ЭПЗ". Модель "Точка зрения" позволила нам учить детей строить ценностную шкалу (рис.9), исследуя характеры героев художественных произведений [20].
|
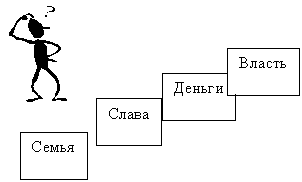
Рис.9. Лестница ценностей героя |
2.4 Системный оператор
2.4.1 ОПИСАНИЕ МОДЕЛИ
Определения
Система - совокупность элементов, обладающая свойством, не сводящимся к сумме свойств отдельных элементов. (Его называют системным свойством).
Функция - здесь - цель, назначение системы.
Подсистема - часть системы.
Надсистема - система, частью которой является данная система.
Антисистема - система, противоположная данной по значению признака, существенного с точки зрения рассматриваемой проблемы.
|
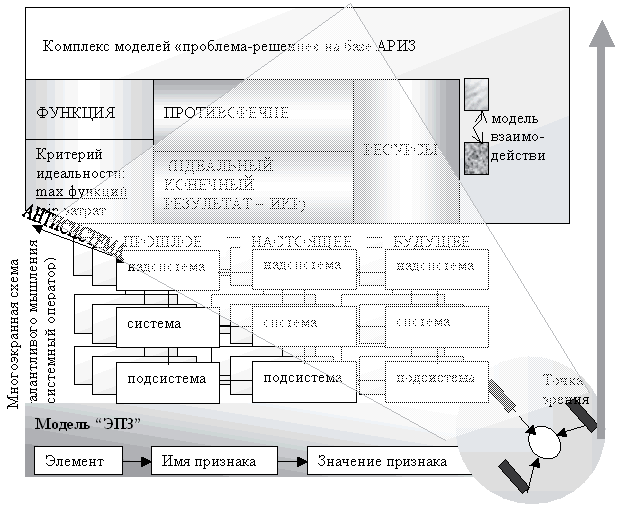
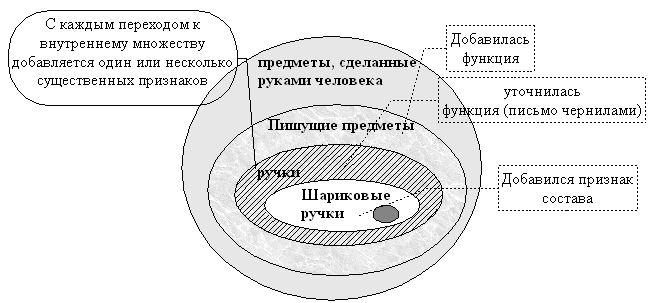
Системный оператор (СО, 2-е его название - "Многоэкранная схема талантливого мышления") формирует системный взгляд на объекты окружающего мира. За внешней простотой этой модели скрываются удивительные возможности.
Грамотное использование системного оператора открывает практически все грани в работе с проблемой, как в логическом аспекте, так и в аспекте воображения. Не случайно главный инструмент ТРИЗ - Алгоритм решения изобретательских задач - автор ТРИЗ Г.С. Альтшуллер называл "многоэкранной схемой, вытянутой в линию". Вероятно, по этой причине, полного и подробного описания использования СО в литературе не существует. Наиболее точное представление об этой модели дано в работе автора ТРИЗ [1] .
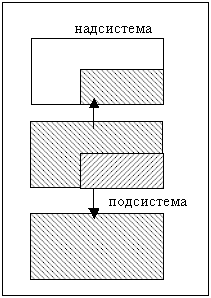
Рис.1.
|
"Технические системы существуют не сами по себе. Каждая из них входит в надсистему, являясь одной из ее частей и взаимодействуя с другими ее частями; но и сами системы тоже состоят из взаимодействующих частей - подсистем. Первый признак талантливого мышления - умение переходить от системы к надсистеме и подсистемам. А для этого должны работать три мысленных экрана (рис.1).
Иными словами, когда речь идет о дереве (системе), надо видеть лес (надсистему) и отдельные части дерева (корни, ствол, ветки, листья - подсистемы). Впрочем, этого мало - на каждом этапе необходимо видеть линию развития: прошлое, настоящее и будущее (рис. 2). ... На мысленных экранах талантливого мыслителя постоянно бушуют страсти: сталкиваются противоречивые тенденции, возникают и обостряются конфликты, идет борьба противоположностей... В азарте этой борьбы изображение подчас сменяется анти-изображением...
|
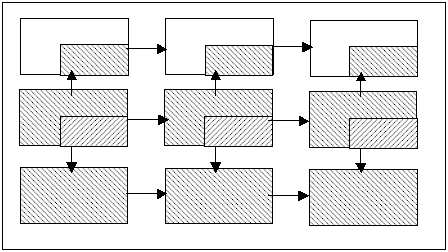
Рис.2.
...Три этажа, девять экранов, изображения и антиизображения - это все-таки предельно упрощенная схема. Настоящее талантливое мышление имеет много этажей вверх от системы (надсистема - наднадсистема -…) и много этажей вниз от системы (подсистема - подподсистема - ...). За деревом надо видеть не только лес, но и биосферу вообще, и не только лист, но и клетку листа. Много экранов должно быть влево от системы (недавнее прошлое, далекое будущее...). Изображение на экранах должно быть то большим, то маленьким, действие то замедляется, то ускоряется...
Сложно? Да, сложно. Мир, в котором мы живем, устроен сложно. И если мы хотим его познавать и преобразовывать, наше мышление должно правильно отражать этот мир. Сложному, динамичному, диалектически развивающемуся миру должна соответствовать в нашем сознании его полная модель - сложная, динамичная, диалектически развивающаяся." ([1], с. 69 - 70).
2.4.2 ПРОИЗВОДНЫЕ МОДЕЛИ И КОНТЕКСТЫ ПРИМЕНЕНИЯ
В обучении используются как полная (отражающая прошлое, настоящее и будущее на различных системных уровнях), так и сокращенные варианты многоэкранной схемы.
2.4.2.1 "Системный лифт"
"Системный лифт" (модель предложена М.С.Гафитулиным) представляет собой вертикаль многоэкранной схемы, использование которой позволяет отследить выполнение функций и проявления различных признаков на разных уровнях системной иерархии (пример - в работе [8 и] на рис.10).
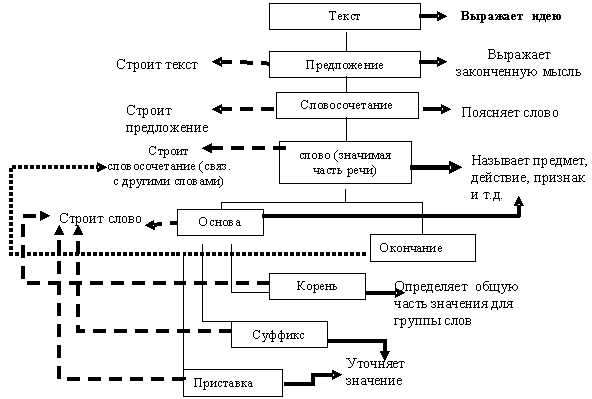
Рис.10. Системный лифт текста
2.4.2.2 Горизонталь системного оператора
Используется:
- для многоуровневой фиксации последовательности событий или сообщений (обычно - заполняется схемами или рисунками);
- в целях создания опоры для составления простого и развернутого плана текста, (обучение пересказу, изложению, конспектированию);
- для фиксации процессов при изучении естествознания (деление клетки и др.);
- при планировании и фиксации этапов процесса эксперимента.
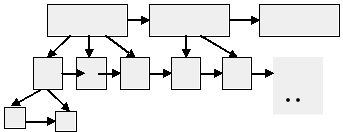
Рис.11. Схема опоры для составления плана текста
2.4.2.3 "Раскадровка"
Раскадровка - это фиксация последовательности событий в схематичных рисунках с обозначение их оценки с позиции каждого участника. Связь кадров дает модель пословицы "Действие -> Результат" (И.Н.Мурашковска, [17]).
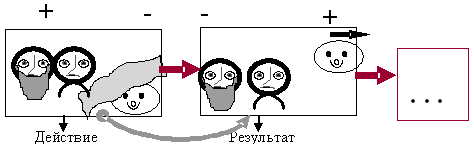
Рис.12. Фрагмент раскадровки сказки "Колобок"
"Плюсами" и "минусами" обозначено отношение героя к зафиксированному в "кадре" событию.
Возможный вариант пословицы, связывающей кадры:
"Кого слишком сильно опекают" -> " - "тот скорей из дома убегает".
Действие -> Результат
2.4.2.4 Модель эмоции
Опираясь на горизонталь СО и "Точку зрения", можно смоделировать некоторые эмоции (удивление, страх, радость,…), как результат оценки человеком ожидаемого и полученного результатов (Рис.13). Мы использовали эту модель в курсе развития речи.
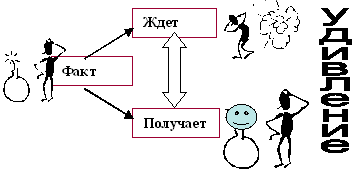
Рис.13. Модель удивления
Следующая группа моделей составлена на основе полной многоэкранной схемы.
2.4.2.5 Универсальный план устного ответа
|
- это схематичная опора для сбора и сообщения информации об изучаемом объекте (на рис.14 - схема, использованная нами. Вариант более развернутой и полной словесной опоры можно найти в работе В.В. Ширяевой [26]).
Схема напоминает ученикам, что, изучая любую систему, следует определить (в контексте интересующих нас проблем) надсистемы, в которые она может входить и их функции, функцию самой системы, ее существенные и характерные признаки, ее эволюцию, состав - и далее повторить этот план для всех основных ее составляющих.
|
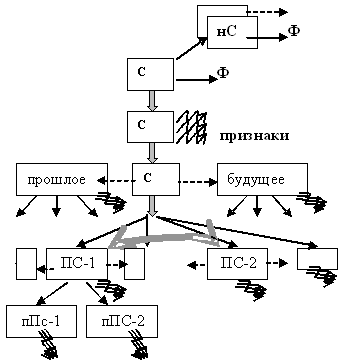
Рис.14. Схема плана устного ответа
|
2.4.2.6 Полная многоэкранная схема конкретной системы ("онтогенез")
Используется в целях:
- исследования эволюции конкретного объекта (характера героя - в гуманитарных курсах, живого организма - в курсе биологии);
- отслеживания связей между различными "экранами";
- выдвижения гипотез;
- объяснения эффектов.
2.4.2.7 Полная многоэкранная схема класса систем ("филогенез")
Позволяет организовать исследование эволюции класса объектов (культурной группы - в гуманитарных курсах [20], живого организма - в курсе биологии [7]).
Более полная многоэкранная схема (рассмотрение системы в онто- и филогенезе, учет антисистем, систем с измененными признаками) используется в исследовательских работах учащихся.
2.5 Комплекс моделей "Проблема-решение"
2.5.1 ОПИСАНИЕ МОДЕЛЕЙ
Данный комплекс моделей предназначен для решения проблемных задач - т.е. задач, способ решения которых неизвестен учащимся.
Для правильного понимания задачи необходимо ее сначала решить: проблемные задачи не могут быть сразу поставлены точно. Процесс решения, в сущности, есть процесс корректировки задачи.
Источником данной группы моделей является центральный инструмент ТРИЗ - Алгоритм решения изобретательских задач (АРИЗ) Г.С.Альтшуллера, предназначенный для решения сложных нетиповых задач [3].
Определения
Функция, ресурсы, идеальность
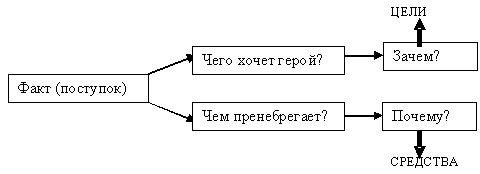
Функция - здесь цель, желаемый результат, который требуется получить в процессе решения проблемы.
Ресурс - запас свойств, возможностей системы, которые могут быть использованы для решения проблемы. Ресурс может быть описан через модель ЭПЗ (набор признаков и диапазоны их возможных значений). Информация о ресурсах системы предполагает знания о явлениях (изменениях значений признаков) и эффектах - комплексах взаимосвязанных явлений.
Критерий идеальности. В соответствии с Законом стремления к идеальности из ТРИЗ [1,2] идеальность можно определить как отношение результативности выполнения функции к "затратности" (ресурсам вещества, энергии, информации, пространства, времени, которые необходимо потратить на выполнение функции).
Инструменты, описывающие модель задачи
Конфликтующая пара и взаимодействие. Согласно ТРИЗ модель минимальной технической системы можно представить как 2 элемента ("вещества" в терминологии ТРИЗ) и их взаимодействия - "поля". При этом один элемент подвергается воздействию, обработке (он является "изделием"), другой - совершает это воздействие (является "инструментом"). При построении модели задачи выявляют конфликтующую пару и типы взаимодействий.
Если эти взаимодействия оценить с позиции "решателя" проблемы как полезные (+) и вредные (-), то получим описание модели задачи в виде системы противоречий. Аналогичная ситуация возникает и при решении нетехнических задач.
Противоречие в ТРИЗ - противоположные требования к одному элементу или признаку, обоснованные в соответствии с результатом, который необходимо получить, решая проблему.
Инструменты, описывающие модель решения
Модель решения - это фактически идеальный образ того ресурса, который мы ищем для решения задачи. Строя абстрактную модель решения, мы набираем значения признаков, которые необходимо получить для достижения требований, сформулированных в модели задачи.
Модель решения в виде идеального конечного результата (ИКР) строится на базе модели задачи из соображений: противоположные требования (полезные значения разных признаков) удовлетворяются или противоположные значения одного признака совмещаются без дополнительных затрат.
Следующий инструмент для получения модели решения - способы разрешения противоречий (сочетания противоположностей).
|
При работе с проблемой процессы построения модели задачи, построения модели решения и конкретизации этих моделей за счет привлечения и преобразования ресурсов системы тесно связаны между собой и идут фактически параллельно. По этой причине здесь рассматривается именно комплекс моделей. Оправданное обособленное их использование встречается достаточно редко.
Минимально необходимый набор шагов по обработке проблемы отражен в адаптированном алгоритме Т.А.Сидорчук и Н.Н.Хоменко, составленном на основе АРИЗ. Обработка проблемы с помощью этого алгоритма предполагает [15]:
- описание проблемной ситуации;
- выделение конкретной задачи из проблемной ситуации;
- построение абстрактной модели задачи в виде противоречия;
- построение абстрактной модели решения (формулировка Идеального Конечного Результата (ИКР), разрешение противоречия);
- конкретизацию модели решения (поиск и преобразование ресурсов);
- оценку результата и при необходимости - переход к другим задачам (по аналогичному плану);
- рефлексию процесса решения.
Приведенные ниже примеры на общеизвестном учебном материале иллюстрируют логику анализа проблемной ситуации с использованием инструментов ТРИЗ.
Пример 1. Проблема написания безударной гласной в корне слова (при условии, что ученикам способ проверки неизвестен).
|
Проблемная ситуация |
Необходимо грамотно писать слова с безударными гласными в корне. |
|
Конкретная задача |
Имеется слово с безударным гласным в корне, которое надо грамотно написать. Чтобы было известно, какой буквой обозначить гласный звук, он должен стоять под ударением - а он безударный. Требуется найти способ проверки орфограммы. |
|
Решение 1 (известное, типовое) |
Дети могут предложить известное им типовое решение - проверку по словарю. |
|
Оценка решения показывает, что оно не подходит. Это позволяет составить модель проблемы в виде системы противоречий. |
|
Модель задачи 1 (в виде системы противоречий из АРИЗ) |
Если проверять слово с сомнительной гласной в корне по словарю, то (+) обеспечим верное написание, но (-) затратим много времени. Если не проверять слово с сомнительной гласной в корне по словарю, то (+) слова сэкономим время, но (-) можем сделать ошибку.. |
|
Модель решения 1 |
Необходимо найти ресурс, который позволит без применения словаря обеспечить верное написание сомнительной гласной в корне слова, не затрачивая на это время. |
|
Ресурсы |
Ресурсами для решения орфографических задач в русском языке могут быть: слова с той же морфемой, в которой возникла задача, соседние с орфограммой буквы или морфемы, соседние слова в предложении с их лексическими значениями. Эффект, который необходим для решения задачи: в русском языке в словах с одинаковым корнем пишется одна и та же гласная (за исключением некоторых специальных случаев). |
|
Уточнение модели решения 1 (идеальный конечный результат - ИКР). |
Другое слово САМО показывает, как надо писать сомнительную гласную, причем делает это мгновенно. |
|
В реальной ситуации на этом этапе ученикам уже понятно решение проблемы. Следующие пункты иллюстрируют возможный вариант более глубокого анализа. |
|
Модель проблемы 2 (в виде противоречия признака аналога физического противоречия из АРИЗ) |
Проверочное слово должно быть таким же, как слово с проверяемой орфограммой, чтобы мы по нему могли узнать, как писать сомнительную букву - и должно быть другим - т.к. в нем соответствующий гласный звук должен стоять под ударением. |
|
Модель решения 2 |
Конкретизируем требования к проверочному слову: оно совпадает с проверяемым словом частично (по корню), но в нем соответствующий гласный стоит под ударением. |
Пример 2. Проблемная ситуация, возникающая при переоткрытии младшими школьниками понятия мерки.
|
Проблемная ситуация |
Мерка - величина, позволяющая измерять размер (в нашем случае - длину) объектов. В принципе мерка может быть любой, для сравнения величин важно, чтобы, различные объекты измерялись одинаковой меркой. Дети проводят измерения и фиксируют, сколько раз данная мерка укладывается по длине в измеряемом объекте. Допустим, в качестве измерителя решили выбрать ленту определенной длины. Тогда возникают сложности при измерении объектов малой длины. |
|
Конкретная задача |
Имеются объекты разной длины: большой и малой и измеритель (мерка). Мы хотим использовать большую мерку, но при этом не можем измерять точно маленькие величины. |
|
Модель задачи в виде противоречия признака |
Мерка должна быть большой, чтобы обеспечить скорость и удобство сравнения и должна быть маленькой, чтобы обеспечить точность. |
|
Модель решения |
ИКР |
Измеритель сам показывает маленькие мерки, оставаясь при этом большим для удобства измерения. |
| |
Разрешение противоречия |
Каждая часть мерки - маленькая, а целая мерка - большая. Большая мерка состоит из некоторого числа маленьких. |
Терминология классической ТРИЗ позволяет описать проблемы, возникающие в технических системах. Для описания проблем независимо от области знаний в ОТСМ-ТРИЗ используется модель Элемент-Признак - Значение (ЭПЗ). Ниже даны формулировки противоречий и ИКР в АРИЗ и их аналоги в терминах модели ЭПЗ.
|
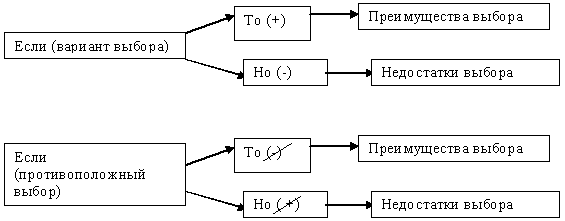
Формулировка системы противоречий в АРИЗ |
Если <условие>, И наоборот: |
то <положительный результат (+)>, |
но <отрицательный результат (-)>. |
|
Если <противоположное условие>, |
то <отсутствует отрицательный результат (нет -)>, |
но <отсутствует положительный результат (нет +)>. |
|
Пример (здесь и ниже приведено только одно из пары противоречий) |
Если проверять сомнительную букву в слове по словарю, |
то обеспечим верное написание сомнительной буквы, |
но проверка будет долгой. |
|
Формулировка противоречия в модели ЭПЗ |
Если <значение признака 3> |
то <позитивное / полезное значение признака 1> |
но <негативное /вредное значение признака 2> |
|
Пояснение примера в модели ЭПЗ |
Признак 3 - способ проверки сомнительной буквы, значение признака - проверка по словарю. |
Признак 1 - правильность написания сомнительной буквы, значение - наличие. |
Признак 2 - время проверки, значение - время велико (более конкретное значение в данном случае неважно). |
|
Модель решения (ИКР) АРИЗ |
икс-элемент, абсолютно не усложняя систему и не вызывая вредных явлений, |
устраняет (указать вредное действие) в течение оперативного времени (ОВ) в пределах оперативной зоны (ОЗ), |
сохраняя способность инструмента совершать (указать полезное действие). |
|
Формулировка в модели ЭПЗ |
Обеспечивает наличие в одном элементе положительных / полезных значений признака 1 и признака 2 |
Рис. 15. Противоречия элемента (система технических противоречий из АРИЗ)
Еще один вид модели проблемы - противоречие признака или физическое противоречие в АРИЗ.
|
Формулировка противоречия из АРИЗ [3] |
“оперативная зона в течение оперативного времени должна |
(указать физическое макросостояние, например, "быть горячей"), чтобы выполнять (указать одно из конфликтующих действий), |
и должна (указать противоположное физическое макросостояние, например, "быть холодной"), чтобы выполнять (указать другое конфликтующее действие или требование). |
|
Формулировка противоречия в модели ЭПЗ |
в заданных условиях (при заданных значениях некоторых признаков) |
признак Х должен иметь значение →, чтобы обеспечить / удовлетворить требование 1 (полезное значение признака 1). |
признак Х должен иметь противоположное значение ←, чтобы обеспечить / удовлетворить требование 2 (полезное значение признака 2). |
|
Пример |
Мерка |
должна быть большой, чтобы обеспечить скорость и удобство сравнения |
и должна быть маленькой, чтобы обеспечить точность. |
|
Модель решения (ИКР) для данного вида противоречия (АРИЗ) |
оперативная зона (указать) в течение оперативного времени (указать) |
должна сама обеспечивать (указать противоположные физические макро- или микросостояния). |
|
ИКР в терминах модели ЭПЗ |
Элемент (ресурс) |
должен сам обеспечивать противоположные значения признака Х. |
|
Пример |
Измеритель САМ |
показывает и большие, и маленькие мерки. |
Рис. 16. Противоречие признака (физическое противоречие в АРИЗ)
Способы разрешения противоречий
Мы использовали 5 универсальных способов разрешения противоречий (Рис.17).
|
Способ разрешения |
Словесная опора |
Пример |
|
В частях |
Часть →, часть ← |
Современный телевизор: часть экрана показывает один канал, часть - другой. |
|
Во времени |
В одно время →, в другое ← |
Ручка указка (в одно время длинная, в другое - короткая) |
|
В отношениях |
С одной точки зрения →, с другой ← |
Упражнение: для одного - трудное, для другого - легкое |
|
Системные переходы |
Одно → , вместе ← Каждая часть →, целое ← |
Цепь: каждая часть - жесткая, целое - гибкое. |
|
“Снятие противоречия” |
Переход к другой модели: в одной надсистеме слово/знак обозначает одно значение признака 1, а в другой это же слово/знак обозначает другое значение признака 2. |
“Я окончил школу в 200 лет”. Человеку должен быть юным (по смыслу ситуации), а он древний (по сообщению). /Число в 3-й системе счисления. |
Рис.17. Способы разрешения противоречий
2.6 Производные модели и контексты применения
2.6.1 ПРОСТЕЙШАЯ МОДЕЛЬ ВЗАИМОДЕЙСТВИЯ
Эта модель вводится в курсе развития речи для обучения дошкольников и младших школьников построению полных предложений. И.Н. Мурашковска в методике обучения составлению описаний [16] дает очень действенную игру, позволяющую "связывать все со всем" и называть взаимодействия (рис.18).
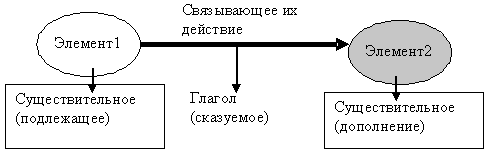
Рис.18. Модель взаимодействия
Рассматривая картинку, дети рисуют в кружках ее элементы, а потом соревнуются, кто сможет "связать" больше кружочков. Для связи вводится простое правило: надо сказать, "что один элемент делает другому" (т.е. указать взаимодействие, тем самым построив полное предложение).
В курсе физики при изучении физических приборов мы использовали классические "вепольные" (от "вещество" и "поле") модели из ТРИЗ, в гуманитарных курсах использовали модель межличностного конфликта, но это - тема отдельной работы, которую нет возможности затронуть здесь.
2.6.2 ФОРМУЛИРОВАНИЕ И РЕШЕНИЕ ПРОБЛЕМ В УЧЕБНОМ МАТЕРИАЛЕ
Примеры использования моделей из АРИЗ при решении учебных задач можно найти в ряде работ по ТРИЗ-педагогике, в частности, в [6,10,12].
Мы в учебном процессе использовали весь комплекс "ПРОБЛЕМА-РЕШЕНИЕ", но противоречие чаще формулировали в виде "противоречия признака":
<Признак … элемента …> должен иметь значение →, чтоб обеспечить (+ ) и должен иметь значение ←, чтоб избавиться от (- ).
В зависимости от знаний ученика, решающего задачу, ему приходится сталкиваться либо с мнимым противоречием (проявлением ПИ), либо с реальным противоречием (в учебной задаче - ресурс для решения есть, но ученику он не известен).
2.6.2.1 Задачи с мнимым противоречием
"Назовите существительное женского рода, оканчивающееся на шипящий звук, но не имеющее в написании мягкого знака на конце".
Противоречие: в существительном женского рода, оканчивающемся на шипящий должен быть "Ь" на конце (по правилу) - и не должно быть "Ь" по условию задачи.
Более внимательный анализ покажет, что это противоречие мнимое: левую часть (правило) необходимо достроить "в существительном женского рода, единственного числа после шипящих пишется "Ь"! Но про единственное число в нашем случае ничего не сказано.
2.6.2.2 Задачи с реальным противоречием
Другой вариант: противоречия: в предложении "Растение росло в саду" первые 2 слова должны иметь одну и ту же гласную в корне, т.е. они являются однокоренными, и имеют различные гласные (можно проверить по словарю) может подвести к изучению новой темы.
2.6.2.3 Распространенное применение идеи противоречия: противоречие "умею - не умею"
Нужно вычислить площадь треугольника (5 класс). Возможные рассуждения: "Мы не умеем вычислять площадь треугольника. Но мы умеем вычислять площадь прямоугольника. Как сделать, чтоб вычислять площадь прямоугольника, а получить площадь треугольника? Привычка к такого рода схеме рассуждений помогает решать проблемы в различных учебных курсах.
|












 вверх
вверх